NCERT Solutions for Class 10 Chapter 11-Electricity
Best NCERT Solutions for Class 10 Science Chapter 11 Electricity .One essential type of energy that drives our contemporary world is electricity. Electricity is essential to daily living and the growth of technology, being used for everything from illuminating our houses to powering intricate machinery. to understand how different devices work and how energy is transmitted and used, one must have a basic understanding of electricity.
Intext Exercise 1
1. What Does an Electric Circuit Mean?
Answer: A continuous, closed path for an electric current is called an electric circuit.
There are several different electric devices in the circuit.
2. Define the Unit of Current.
Answer: A single coulomb of charge flowing every second equals one ampere. that is,
3. Calculate the Number of Electrons Constituting One Coulomb of Charge.
Answer:
One electron has a charge of n×e, or 1.6 × 10−19 C.
Let’s say that
One coulomb is made of electrons.
Consequently, n=1 ⇒n=1(1.6×10−19) ⇒n=6.25×1018
Therefore, 6.25×1018 electrons make up one coulomb of charge.
Intext Exercise 2
1. Name a Device That Helps To Maintain a Potential Difference Across a Conductor.
Answer: Potential difference across a conductor and in a circuit can be maintained by any device, such as a battery or cell.
2. What Is Meant by Saying That the Potential Difference Between Two Points is
?
Answer: It indicates that transporting one C charge from one location to another requires one J of work.
3. How Much Energy Is Given to Each Coulomb of Charge Through a
battery?
Answer:
By calculating the work a charge does in the circuit, we can determine the energy provided to it.
Work Done = Potential Difference × Charg gives the amount of work completed in the circuit.
Whereas
One charge is equal to one C.
Potential disparity is equal to 6 V.
Task Completed = 6 × 1 = 6 J
Thus, 6J
is allocated to each coulomb of charge travelling through a 6 V battery.
Intext Exercise 3
1. On What Factors Does the Resistance of a Conductor Depend?
Answer:
A conductor’s resistance is determined by the following factors:
The conductor’s length (l)
Area across the conductor’s cross-section (A)
The conductor’s nature (ρ) and temperature (T) are related to each other.
2. Will Current Flow More Easily Through a Thick Wire or a Thin Wire of the Same Material, When Connected to the Same Source? Why?
Answer:
The following represents the relationship between resistance and cross section area: R∧1A
The resistance of a wire is directly proportional to its cross-sectional area. The stream rises as the resistance falls.
Less current will flow through thinner wires whereas more current will flow through thicker wires.
3. Let the Resistance of an Electrical Component Remain Constant While the Potential Difference Across the Two Ends of the Component Decreases to Half of Its Former Value. What Change Will Occur in the Current Through It?
Answer:
Ohm’s law provides the change in the current passing through the component as,
V=IR ⇒ I=VR
where R is the electrical component’s resistance.
The current is V, which is the potential difference.
When halving the potential difference while maintaining R
identical, I2=V2R, where V2=V2 ⇒I2=V2R; nevertheless, we are aware that I=VR ⇒I2=I2.
That is, half of the current is lost.
4. Why are Coils of Electric Toasters and Electric Irons Made of an Alloy Rather Than a Pure Metal?
Answer:
The alloys are crafted so that they have a higher resistivity than metals. Furthermore, they don’t melt in hot weather.
5. Use the Data in Table To Answer the Following:
Table: Electrical resistivity of some substances at
|
Material |
Resistivity ΩmΩm |
|
|
Conductor |
Silver |
1.60×10−81.60×10−8 |
|
Copper |
1.62×10−81.62×10−8 |
|
|
Aluminium |
2.63×10−82.63×10−8 |
|
|
Tungsten |
5.20×10−85.20×10−8 |
|
|
Nickel |
6.84×10−86.84×10−8 |
|
|
Iron |
10.0×10−810.0×10−8 |
|
|
Chromium |
12.9×10−812.9×10−8 |
|
|
Mercury |
94.0×10−894.0×10−8 |
|
|
Manganese |
1.84×10−81.84×10−8 |
|
|
Alloy |
Constantan (alloy of Cu and Ni) |
44×10−644×10−6 |
|
Manganin (alloy of Cu, Mn and Ni) |
49×10−649×10−6 |
|
|
Nichrome (alloy of Ni, Cr, Mn and Fe) |
100×10−6100×10−6 |
|
|
Insulator |
Glass |
1010∼10141010∼1014 |
|
Hard rubber |
1013∼10161013∼1016 |
|
|
Ebonite |
1015∼10171015∼1017 |
|
|
Diamond |
1012∼10131012∼1013 |
|
|
Paper (Dry) |
10121012 |
a) Which Among Iron and Mercury is a Better Conductor?
Answer:
Iron has a resistivity of 10.0×10−8Ωm.
Mercury’s resistivity is 94.0×10−8Ωm.
Mercury has a higher resistance than iron. Because resistivity and conductivity are inversely correlated, iron is a better conductor than mercury.
b) Which Material is the Best Conductor?
Answer:
The best conductor is a metal with the lowest resistance. In the preceding
Inquiry: Based on the chart, silver is the most effective conductor.
Intext Exercise 4
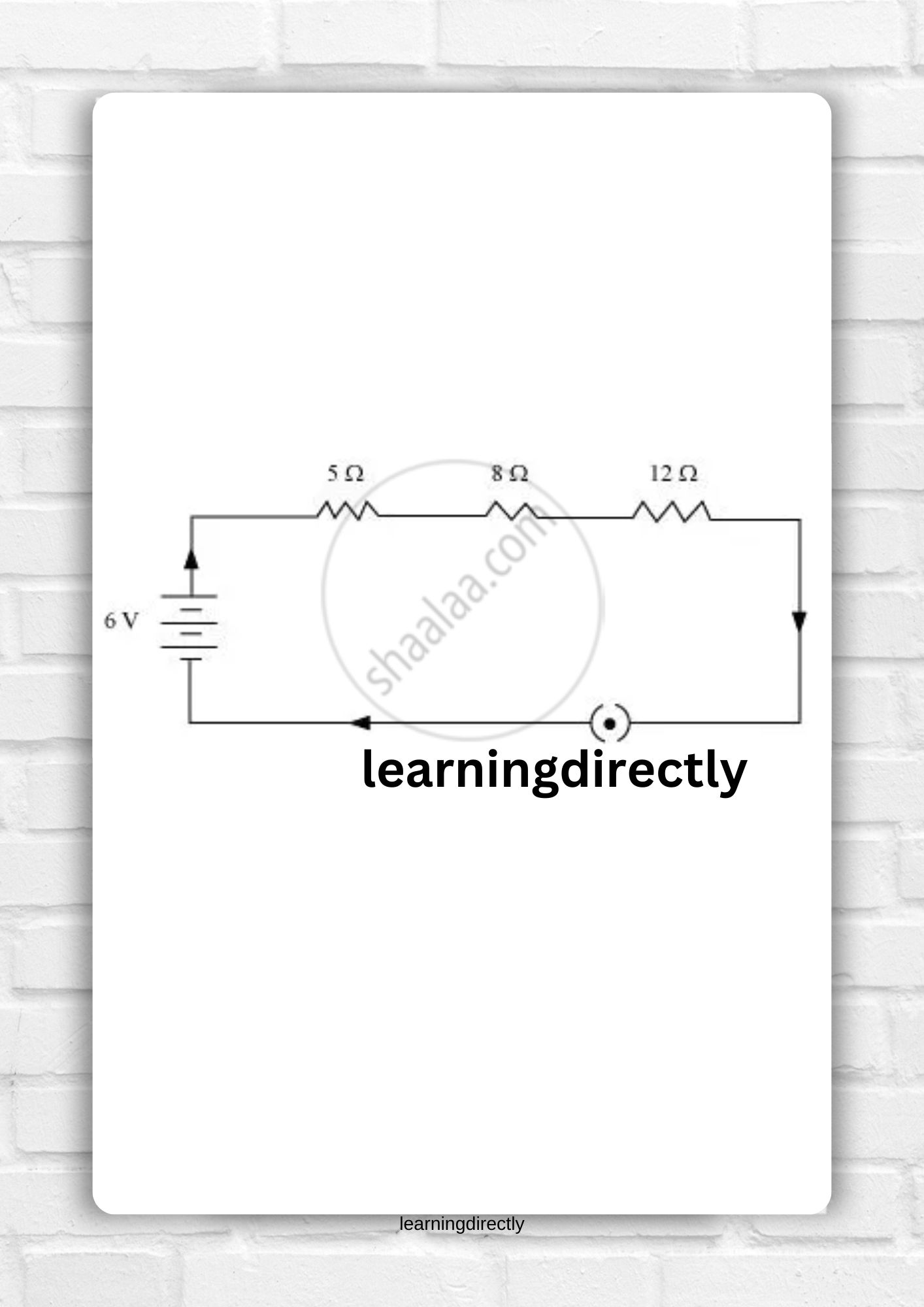
1. Draw a Schematic Diagram of a Circuit Consisting of a Battery of Three Cells of
each, a
resistor, an
resistor, and a
resistor, and a Plug Key, All Connected in Series.
Answer:
The circuit design that follows displays three resistors with resistances of 5 Ω, 8 Ω, and 12 Ω.
correspondingly linked in series with a 6 V potential battery

2. Redraw the Circuit of Question 11, Putting in an Ammeter To Measure the Current Through the Resistors and a Voltmeter To Measure Potential Difference Across the
resistor. What Would Be the Readings in the Ammeter and the Voltmeter?
Answer: To measure the current passing through the resistors in the circuit, an ammeter needs to be connected in series with them.
In order to quantify the potential differential over the 12 Ω
voltmeter, which needs to be wired in parallel across the 12 Ω resistor
resistor, as the illustration below illustrates.
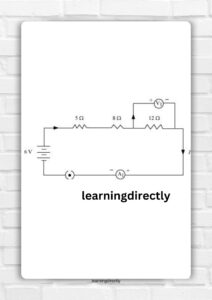
Let’s determine the circuit’s total current. That and the current flowing through each resistor and the ammeter ought to match.
Since Req = R1 + R2 + R3 ⇒Req = 5 + 8 + 12 ⇒Req = 25\�, Ieq = VReq ⇒Ieq = 625 = 0.24 A
The ammeter will thus show 0.24A.
The voltage across R3= V3 is equal to Ieq×R3 ⇒V3=0.24×12 ⇒V3=2.88.
The voltmeter will therefore display 2.88V.
Intext Exercise 5
1. Judge the Equivalent Resistance When the Following Are Connected in Parallel:
a)
and
Answer:
We can say that comparable resistance is less than the least resistance in a parallel connection.
Thus, the resistance in both scenarios should be less than 1Ω.
.. These claims can be verified using the methods listed below:
When one Ω
and 106 Ω
are parallelly connected:
Allow R
be the corresponding amount of resistance.
1R=11+1106 ⇒ R=106106+1≈106106 ⇒ R=1Ω
Equivalent resistance is therefore less than 1 Ω.
b)
and
Answer:
In the event that 1 Ω, 103Ω, and 106Ω are linked in parallel:
Allow R
be the corresponding amount of resistance.
R=10000001000001=0.999Ω 1R=11+1103+1106=106+103+1106
Consequently, 0.999 Ω is the corresponding resistance.
, or less than one volt.
2. An Electric Lamp of
, a Toaster of Resistance
, and a Water Filter of Resistance
are Connected in Parallel to a
Source. What is the Resistance of an Electric Iron Connected to the Same Source That Takes as Much Current as all Three Appliances, and What is the Current Through it?
Answer:
Considering that,
Electric lamp resistance, R1 = 100 Ω
Toaster resistance, R2 = 50 Ω
Water filter resistance, R3 = 500 Ω
The source’s voltage, V = 220 V
Let R represent the circuit’s equivalent resistance.
R=50016Ω, where 1R=1R1+1R2+1R3=1100+150+1500=5+10+1500=16500.
V = IR ⇒I=VR where I is the current flowing through the circuit and I = 22050016 = 200×16500 = 6.4A, according to Ohm’s law.
Therefore, the three appliances in question draw 6.4 A of current together.
As a result, current drawn from an electric iron linked to the same potential source (220 V)
= 6.4 A
Assume R ′
be the electric iron’s resistance. In line with Ohm’s law,
V is equal to I{R}’
⇒R′ = VI = 2206.4 = 34.375Ω
As a result, 34.375 Ω is the electric iron’s resistance.
and 6.4A of current is passing through it.
3. What Are the Advantages of Connecting Electrical Devices in Parallel With the Battery Instead of Connecting Them in Series?
Answer:
The same voltage is supplied to each device via a parallel connection.
Failure of one device results does not disturb the full circuit.
There is less resistance overall.
4. How Can Three Resistors of Resistances
and
be Connected to Give a Total Resistance of
a)
Answer:
Three resistors with resistances of 2 Ω, 3 Ω, and 6 Ω are present.
Examine the circuit below:
Here,
and 3 Ω
Resistors have parallel connections.
Therefore, 1R=1R1+1R2 will provide their equivalent resistance.
⇒R=116+13=6×36+3=2Ω
This mixture is linked to a 2 Ω
resistor connected in series.
Consequently, the circuit’s equivalent resistance is equal to 2 Ω + 2 Ω = 4 Ω.
Therefore, the circuit’s total resistance is 4 Ω.
b)
Answer:
The three resistors’ connections are shown in the circuit schematic that follows.
Every resistor has a parallel connection. Consequently, their corresponding resistance will be provided as
R = 112+13+16 = 13+2+16 = 66=1\�
Consequently, the circuit’s total resistance is 1 Ω.
5. What is
a) The Highest Total Resistance that can be Secured by Combinations of Four Coils of Resistance
?
Answer:
Four coils with resistances of 4 Ω, 8 Ω, 12 Ω, and 24 Ω are present, in that order.
We must join these resistances in sequence to obtain the maximum resistance. They have an equivalent resistance of 4 + 8 + 12 + 24 = 48 Ω.
b) The Lowest Total Resistance that can be Secured by Combinations of Four Coils of Resistance
?
Answer:
Connect them in parallel to get the least resistance.
In this instance, Req
is as follows: Req=114+18+112+124=16+3+2+124=2412=2Ω. As a result, the lowest equivalent resistance that may be achieved is 2 Ω.
Intext Exercise 6
1. Why Does the Cord of an Electric Heater Not Glow While the Heating Element Does?
Answer:
A system’s capacity to produce heat is directly related to its resistance.
Because the heating element has more resistance, more heat is generated, which causes it to glow.
Additionally, the wire has less resistance, which results in less heat being created. As a result, the heating element glows while the wire does not.
2. Compute the Heat Generated While Transferring 9600096000 coulomb of Charge in One Hour Through a Potential Difference of 50 V50 V.
Answer:
The Joule’s law of heating provides the amount of heat (H) produced as
Where, voltage, V= 50 V, and H = VIt
The time is t = 1 h = 1 × 60 × 60 s.
H = V.I. t ⇒H = V⋅qt⋅t ⇒H = V⋅q
⇒H=50×96000
⇒H=4.8×106J
Consequently, H=4.8×106J of heat is created during the charge transfer.
3. An Electric Iron of Resistance 20 Ω 20 Ω Takes a Current of 5 A5 A . Calculate the Heat Developed in 30 s30 s.
Answer:
According to Joule’s law of heating, the amount of (H) heat produced is H=VIt=I2Rt.
Whereas
Presently, I equals 5 A
Time, t = 30 s
20Ω is the resistance R.
H=I2Rt ⇒ H=52×20×30
⇒H=1.5×104J
Consequently, H=1.5×104J is the quantity of heat generated in the electric iron.
Intext Exercise 7
1. What Determines the Rate at Which Energy is Delivered by a Current?
Answer:
The rate at which energy is delivered by a current or consumed by the appliance is the power of the appliance.
2. An Electric Motor Takes
from a
line. Determine the Power of the Motor and the Energy Consumed in 22 hrs.
Answer:
The formula for power (P) is P=VI.
where V= 220 V is the voltage and I= 5 A is the current.
220 × 5 = 1100 W is P.
Motor energy consumption = Pŗt
Where, When, P=1100×7200 since t=2h=2×60×60=7200s
Consequently, the motor’s power is equal to 1100 W.
The motor’s energy consumption is 7.92 × 106J.
NCERT Exercise
1. A Piece of Wire of Resistance RR is Cut into Five Equal Parts. These parts are then Connected in Parallel. If the Equivalent Resistance of this Combination is
, then the Ratio
is
a. 125125
b. 1515
c. 55
d. 2525
Answer:
Resistance and current have a relationship that is R∧I.
If the wire is broken into five equal segments, the resistance of each part =R5
Each of the five components is linked in parallel. Equivalent resistance ({R}’) follows.
is stated as
1R′ = 5R+5R+5R+5R+5R= 5+5+5+5+5R= 25R
⇒RR′ = 25
Consequently, the ratio RR′
is 25.
2. Which of the Following Does Not Represent Electric Power in a Circuit?
a.
b.
c. VIVI
d. V2RV2R
Answer:
Option (b) is the right choice.
The formula for electrical power is P=VI…(i)
Ohm’s law states that V = IR. (ii)
Evidently, every other equation—aside from (b)—can be transformed into V I.
3. An Electric Bulb is Rated
and
. When it is operated on
,the Power Consumed Will be
a).
b).
c).
d).
Answer:
The choice (d) is the right response.
The words “energy consumed by an appliance”
P = VI = V2R
If you lower the supply voltage to 110 V, the bulb’s resistance stays the same.
Thus, resistance needs to be identified first.
Given P = 100 W, R=V2P
V equals 220 V ⇒R = (220)2100= 484Ω
Currently, if the lightbulb is using 110 V
, then the power expression provides the energy that it uses as
⇒ P′ = (V′)2R = (110)2484 = 25W
4. Two Conducting Wires of the Same Material and of Equal Lengths and Equal Diameters Are First Connected in Series and Then Parallel in a Circuit Across the Same Potential Difference. The Ratio of Heat Produced in Series and Parallel Combinations Would be
a).
b).
c).
d).
Answer:
The right response is option (c), as the ratio of heat produced in series and parallel combinations would be 1:4.
Regarding the same V
and t
the proportion of heat generated in series HS
to the heat generated in parallel HP
is provided by
RPRS=V2RPt=HSHP=V2RSt
Currently, Rs=R+R=2R ⇒Rp=11R+1R=R2.
Thus, the ratio:
HSHP=R22R=14
As a result, the heat generated in parallel and series combinations is 1:4.
5. How is a Voltmeter Connected in the Circuit To Measure the Potential Difference Between Two Points?
Answer:
In order to measure the potential difference between two places, the voltmeter needs to be linked in parallel.
This is so that the voltmeter can measure the voltage across the parallel circuit.
On the other hand, voltmeters are not useful for a series circuit. In a series circuit, an ammeter is utilised instead.
6. A Copper wire has Diameter
and resistivity of
What Will be the Length of this Wire to Make its Resistance
? How Much Does the Resistance Change if the Diameter is Doubled?
Answer:
A copper wire with a length of lm and a cross-section of Am2 has resistance (R).
is provided by the formula R=ρlA.
Whereas
Copper’s resistivity, ρ=1.6×10−8Ω m
Area of cross-section of the wire, A=π(Diameter2)2.
Circumference: 0.5 mm / 0.0005 m
R= 10 Ω is the resistance.
Thus, the wire’s length, l=RAρ=10×3.14×(0.0052)21.6×10−8=10×3.14×254×1.6=122.65m, may be determined.
Should the wire’s diameter double, the new diameter D′ would be 2×0.5=1mm=0.001 m.
Let’s now determine the new resistance using a diameter that is double the previous one. that is,
D′=2D ⇒ A′=p (D′/2)2=4A
New resistance will now likewise be decreased four times.
Since {R}’ = R/4, {R}’ = 10/4 = 2.5 Ω
Consequently, the wire’s length is 122.65 meters.
and 2.5 Ω is the new resistance.
7. The Values of Current II Flowing in a Given Resistor for the Corresponding Values of Potential Difference VV Across the Resistor are Given Below:
|
II(ampere) |
0.50.5 |
1.01.0 |
2.02.0 |
3.03.0 |
4.04.0 |
|
VV(volts) |
0.50.5 |
3.43.4 |
6.76.7 |
10.210.2 |
13.213.2 |
Plot a Graph Between VV and II and Calculate the Resistance of That Resistor.
Answer:
The indicator-volt characteristic is the plot of voltage against current.
Plotting is done with the voltage on the x-axis and the current on the y-axis.
The provided table displays the current values for various voltage settings.
|
VV (volts) |
1.61.6 |
3.43.4 |
6.76.7 |
10.210.2 |
13.213.2 |
|
II (ampere) |
0.50.5 |
1.01.0 |
2.02.0 |
3.03.0 |
4.04.0 |
The resistance (R) value can be found by calculating the slope of the line: slope = 1R=BCAC=26.8R=6.82=3.4
Consequently, the resistor’s resistance is 3.4 Ω.
8. When a
Battery is Connected Across an Unknown Resistor, There is a Current of
in the Circuit. Find the value of the Resistance of the Resistor.
Answer:
Ohm’s law provides the resistance (R) of a resistor as follows:
V = IR ⇒R = VI
Where the circuit’s current, I = 2.5 mA = 2.5 × 10-3A, and the potential difference, V = 12 V
R = 122.5×10−3 = 4.8×103Ω = 4.8 kΩ
4.8 k Ω is the resistor’s resistance as a result.
9. A Battery of
is Connected in Series with Resistors of
and
, respectively. How Much Current Would Flow through the
resistor?
Answer:
Because everything is connected in series, the same current should pass through all of the resistances and the circuit.
V equals IR.
⇒R=VI
R is the corresponding resistance in this case.
The resistances added together will equal the value of R.
R = 0.2 + 0.3 + 0.4 + 0.5 + 12 = 13.4 Ω
Potential disparity, V = 9 V ⇒I = 913.4 = 0.671A
Consequently, the current that would pass via the 12 Ω
It is a 0.671 A resistor.
10. How Many
resistors (in parallel) are Required to carry
on a
Line?
Answer:
Assume for the moment that there are x resistances.
When resistors are connected in parallel, their equivalent resistance is determined by
1R = x×1176 ⇒ R = 176x
Ohm’s law is now expressed as V=IR ⇒R=VI.
When the current is I = 5 A and the supply voltage is V = 220 V.
The equation is therefore 176x=2205 ⇒x=17644 ⇒x=4.
Consequently, four 176 Ω resistors
are needed to draw the specified quantity of current.
11. Show How You Would Connect Three Resistors, Each of Resistance
, so that the combination has a resistance of
Answer.
Two Resistors in Parallel: Consider the following figure.
A pair of 6 Ω resistors is linked in parallel. Their corresponding resistance is going to be
R=116+16=6×66+6=3Ω
The third six inches
Three Ω is linked in series with the resistor.
Thus, 6 Ω + 3 Ω = 9 Ω is the circuit’s equivalent resistance.
b).
Two Resistors in Series: Consider the following figure.
Two
resistors are connected in series.
The total R=6+6=12Ω will be their corresponding resistance.
The third six inches
Since the resistor and 12 Ω are connected in parallel, the equivalent resistance is $\\{R}_{eq}}=\frac{1}{\frac{1}{12}+\frac{1}{6}}=\frac{12\time
$\Omega $ 6}{12+6}=4
Consequently, 4 Ω is the overall resistance.
..
12. Several Electric Bulbs Designed to be Used on a
Electric Supply Line, are Rated
. How Many Lamps can be Connected in Parallel with Each Other Across the Two Wires of
line if the maximum allowable current is
?
Answer:
The formula for one bulb’s resistance, R1, is P1=V2R1⇒R1=V2P1.
where V = 220 V is the supply voltage.
Maximum current permitted, I = 5 A
An electric bulb’s rating is P1 = 10 W.
One bulb’s resistance is given by R1=(220)210=4840Ω.
Use Ohm’s law on the circuit that has every bulb in it.
The total resistance of the circuit for x number of electric lights is given by V = IR R.
⇒R=VI=2205=44Ω
Every electric bulb has a resistance of R1 = 4840 Ω.
Clearly, 1R=1R1×x ⇒x=R1R=484044=110 when the resistors are connected in parallel.
Consequently, 110
It is possible to connect electric lamps in parallel.
13. A Hot Plate of an Electric Oven Connected to a
Line has Two Resistance Coils AA and BB , Each of
Resistances, Which May be Used Separately, in Series, or in Parallel. What are the Currents in the Three Cases?
Answer:
The given data in the question is as follows:
Supply voltage,
.
Resistance of one coil,
.
a) Coils are Used Separately:
According to Ohm’s law,
V is equal to I1R1.
where I1 represents the coil’s current flow.
⇒I1 = VR1 = 22024 = 9.166A
Consequently, 9.16 A
When utilised independently, each coil will experience current flow.
b) Coils are Connected in Series:
R2 = 24 Ω + 24 Ω = 48 Ω is the total resistance.
Ohm’s law states that V=I2R2.
where I2 represents the current passing through the circuit in series.
⇒I2=VR2=22048=4.58A
Thus, 4.58 A
In a circuit when the coils are connected in series, current will flow.
c) Coils are Connected in Parallel:
The formula for total resistance, R3, is R3=1124+124=242=12 Ω.
Ohm’s law states that V=I3R3.
where the circuit’s current, I3, is expressed.
⇒22012=18.33A=I3=VR3
Consequently, 18.33 A
In a circuit with coils connected in parallel, current will flow.
14. Compare the Power Used in the
Resistor in Each of the Following Circuits:
a).
battery in series with
and
resistors, and
Answer:
The answer to the question is V = 6 V 1 Ω and 2 Ω.
Resistors have a series connection.
Consequently, the circuit’s equivalent resistance, R=1+2=3 Ω
Ohm’s law states that V = IR.
where I is the circuit’s current ⇒I = 63= 2 A
In series, the circuit as a whole experiences the same current flow.
Current therefore passing through the two Ω
There is a 2 A resistor.
Strength comes from the phrase,
P=I2R = 22× 2 = 8 W
b).
battery in parallel with
and
resistors.
Answer:
Potential difference between 12 Ω and 2 Ω, V = 4 V
Resistors have parallel connections.
Every element in a parallel circuit experiences the same voltage across it. Thus, the voltage between two ohms
There will be a 4 V resistor.
The amount of power that a 2 Ω resistor uses is determined by
P=V2R=422= 8 W
Consequently, the power consumed by 2 Ω
It has an 8W resistor.
Best NCERT Solutions for Class 10 Science Chapter 11 Electricity
For the Next Poem Solution Click Below
CHAPTER 1 – Chemical Reactions and Equations
CHAPTER 2 – Acid, Bases and Salts
CHAPTER 3 – Metals and Non-metals
CHAPTER 4 – Carbon And Its Compounds
CHAPTER 6 – Control And Coordination
CHAPTER 7 – How do Organisms Reproduce
CHAPTER 8 – Heredity and Evolution
CHAPTER 9 – Light Reflection and Refraction
CHAPTER 10 – The Human Eye and the Colourful World
CHAPTER 12 – Magnetic Effects of Electric Current
For more updates, you can follow us on our social media