NCERT Solution for Class 9 Maths Chapter 2: Polynomials offers comprehensive and detailed answers to all the exercises in the chapter. This resource helps students grasp key concepts such as polynomial expressions, degrees, and theorems with clarity. It includes step-by-step solutions to enhance understanding and problem-solving skills. Designed to align with the NCERT curriculum, this guide supports students in mastering polynomials, ensuring a solid foundation for advanced mathematics topics. Ideal for exam preparation and homework assistance, it provides clear explanations and practical examples to boost confidence and performance.
Here Are The Ncert Solution For Class 9 Maths
Chapter – 2 Polynomials
Exercise 2.1
Question 1. Which of the following expressions are polynomials in one variable, and which are not? State reasons for your answer.
(i) 4x2–3x+7
Solution:
The equation 4x2–3x+7 can be written as 4x2–3x1+7x0
Since x is the only variable in the given equation and the powers of x (i.e. 2, 1 and 0) are whole numbers, we can say that the expression 4x2–3x+7 is a polynomial in one variable.
(ii) y2+√2
Solution:
The equation y2+√2 can be written as y2+√2y0
Since y is the only variable in the given equation and the powers of y (i.e., 2 and 0) are whole numbers, we can say that the expression y2+√2 is a polynomial in one variable.
(iii) 3√t+t√2
Solution:
The equation 3√t+t√2 can be written as 3t1/2+√2t
Though t is the only variable in the given equation, the power of t (i.e., 1/2) is not a whole number. Hence, we can say that the expression 3√t+t√2 is not a polynomial in one variable.
(iv) y+2/y
Solution:
The equation y+2/y can be written as y+2y-1
Though y is the only variable in the given equation, the power of y (i.e., -1) is not a whole number. Hence, we can say that the expression y+2/y is not a polynomial in one variable.
(v) x10+y3+t50
Solution:
Here, in the equation x10+y3+t50
Though the powers, 10, 3, 50, are whole numbers, there are 3 variables used in the expression
x10+y3+t50. Hence, it is not a polynomial in one variable.
Question 2. Write the coefficients of x2 in each of the following:
(i) 2+x2+x
Solution:
The equation 2+x2+x can be written as 2+(1)x2+x
We know that the coefficient is the number which multiplies the variable.
Here, the number that multiplies the variable x2 is 1
Hence, the coefficient of x2 in 2+x2+x is 1.
(ii) 2–x2+x3
Solution:
The equation 2–x2+x3 can be written as 2+(–1)x2+x3
We know that the coefficient is the number (along with its sign, i.e. – or +) which multiplies the variable.
Here, the number that multiplies the variable x2 is -1
Hence, the coefficient of x2 in 2–x2+x3 is -1.
(iii) (π/2)x2+x
Solution:
The equation (π/2)x2 +x can be written as (π/2)x2 + x
We know that the coefficient is the number (along with its sign, i.e. – or +) which multiplies the variable.
Here, the number that multiplies the variable x2 is π/2.
Hence, the coefficient of x2 in (π/2)x2 +x is π/2.
(iii)√2x-1
Solution:
The equation √2x-1 can be written as 0x2+√2x-1 [Since 0x2 is 0]
We know that the coefficient is the number (along with its sign, i.e. – or +) which multiplies the variable.
Here, the number that multiplies the variable x2is 0
Hence, the coefficient of x2 in √2x-1 is 0.
Question 3. Give one example each of a binomial of degree 35, and of a monomial of degree 100.
Solution:
Binomial of degree 35: A polynomial having two terms and the highest degree 35 is called a binomial of degree 35.
For example, 3x35+5
Monomial of degree 100: A polynomial having one term and the highest degree 100 is called a monomial of degree 100.
Question 4. Write the degree of each of the following polynomials:
(i) 5x3+4x2+7x
Solution:
The highest power of the variable in a polynomial is the degree of the polynomial.
Here, 5x3+4x2+7x = 5x3+4x2+7x1
The powers of the variable x are: 3, 2, 1
The degree of 5x3+4x2+7x is 3, as 3 is the highest power of x in the equation.
(ii) 4–y2
Solution:
The highest power of the variable in a polynomial is the degree of the polynomial.
Here, in 4–y2,
The power of the variable y is 2
The degree of 4–y2 is 2, as 2 is the highest power of y in the equation.
(iii) 5t–√7
Solution:
The highest power of the variable in a polynomial is the degree of the polynomial.
Here, in 5t–√7
The power of the variable t is: 1
The degree of 5t–√7 is 1, as 1 is the highest power of y in the equation.
(iv) 3
Solution:
The highest power of the variable in a polynomial is the degree of the polynomial.
Here, 3 = 3×1 = 3× x0
The power of the variable here is: 0
Hence, the degree of 3 is 0.
Question 5. Classify the following as linear, quadratic and cubic polynomials:
Solution:
(i) x2+x
Solution:
The highest power of x2+x is 2
The degree is 2
Hence, x2+x is a quadratic polynomial
(ii) x–x3
Solution:
The highest power of x–x3 is 3
The degree is 3
Hence, x–x3 is a cubic polynomial
(iii) y+y2+4
Solution:
The highest power of y+y2+4 is 2
The degree is 2
Hence, y+y2+4 is a quadratic polynomial
(iv) 1+x
Solution:
The highest power of 1+x is 1
The degree is 1
Hence, 1+x is a linear polynomial.
(v) 3t
Solution:
The highest power of 3t is 1
The degree is 1
Hence, 3t is a linear polynomial.
(vi) r2
Solution:
The highest power of r2 is 2
The degree is 2
Hence, r2is a quadratic polynomial.
(vii) 7x3
Solution:
The highest power of 7x3 is 3
The degree is 3
Hence, 7x3 is a cubic polynomial.
Ncert Solution For Class 9 Maths Chapter – 2
Exercise 2.2
Question 1. Find the value of the polynomial (x)=5x−4x2+3.
(i) x = 0
(ii) x = – 1
(iii) x = 2
Solution:
Let f(x) = 5x−4x2+3
(i) When x = 0
f(0) = 5(0)-4(0)2+3
= 3
(ii) When x = -1
f(x) = 5x−4x2+3
f(−1) = 5(−1)−4(−1)2+3
= −5–4+3
= −6
(iii) When x = 2
f(x) = 5x−4x2+3
f(2) = 5(2)−4(2)2+3
= 10–16+3
= −3
Question 2. Find p(0), p(1) and p(2) for each of the following polynomials:
(i) p(y)=y2−y+1
Solution:
p(y) = y2–y+1
∴ p(0) = (0)2−(0)+1 = 1
p(1) = (1)2–(1)+1 = 1
p(2) = (2)2–(2)+1 = 3
(ii) p(t)=2+t+2t2−t3
Solution:
p(t) = 2+t+2t2−t3
∴ p(0) = 2+0+2(0)2–(0)3 = 2
p(1) = 2+1+2(1)2–(1)3=2+1+2–1 = 4
p(2) = 2+2+2(2)2–(2)3=2+2+8–8 = 4
(iii) p(x)=x3
Solution:
p(x) = x3
∴ p(0) = (0)3 = 0
p(1) = (1)3 = 1
p(2) = (2)3 = 8
(iv) P(x) = (x−1)(x+1)
Solution:
p(x) = (x–1)(x+1)
∴ p(0) = (0–1)(0+1) = (−1)(1) = –1
p(1) = (1–1)(1+1) = 0(2) = 0
p(2) = (2–1)(2+1) = 1(3) = 3
Question 3. Verify whether the following are zeroes of the polynomial indicated against them.
(i) p(x)=3x+1, x = −1/3
Solution:
For, x = -1/3, p(x) = 3x+1
∴ p(−1/3) = 3(-1/3)+1 = −1+1 = 0
∴ -1/3 is a zero of p(x).
(ii) p(x) = 5x–π, x = 4/5
Solution:
For, x = 4/5, p(x) = 5x–π
∴ p(4/5) = 5(4/5)- π = 4-π
∴ 4/5 is not a zero of p(x).
(iii) p(x) = x2−1, x = 1, −1
Solution:
For, x = 1, −1;
p(x) = x2−1
∴ p(1)=12−1=1−1 = 0
p(−1)=(-1)2−1 = 1−1 = 0
∴ 1, −1 are zeros of p(x).
(iv) p(x) = (x+1)(x–2), x =−1, 2
Solution:
For, x = −1,2;
p(x) = (x+1)(x–2)
∴ p(−1) = (−1+1)(−1–2)
= (0)(−3) = 0
p(2) = (2+1)(2–2) = (3)(0) = 0
∴ −1, 2 are zeros of p(x).
(v) p(x) = x2, x = 0
Solution:
For, x = 0 p(x) = x2
p(0) = 02 = 0
∴ 0 is a zero of p(x).
(vi) p(x) = lx+m, x = −m/l
Solution:
For, x = -m/l ; p(x) = lx+m
∴ p(-m/l)= l(-m/l)+m = −m+m = 0
∴ -m/l is a zero of p(x).
(vii) p(x) = 3x2−1, x = -1/√3 , 2/√3
Solution:
For, x = -1/√3 , 2/√3 ; p(x) = 3x2−1
∴ p(-1/√3) = 3(-1/√3)2-1 = 3(1/3)-1 = 1-1 = 0
∴ p(2/√3 ) = 3(2/√3)2-1 = 3(4/3)-1 = 4−1 = 3 ≠ 0
∴ -1/√3 is a zero of p(x), but 2/√3 is not a zero of p(x).
(viii) p(x) =2x+1, x = 1/2
Solution:
For, x = 1/2 p(x) = 2x+1
∴ p(1/2) = 2(1/2)+1 = 1+1 = 2≠0
∴ 1/2 is not a zero of p(x).
Question 4. Find the zero of the polynomials in each of the following cases:
(i) p(x) = x+5
Solution:
p(x) = x+5
⇒ x+5 = 0
⇒ x = −5
∴ -5 is a zero polynomial of the polynomial p(x).
(ii) p(x) = x–5
Solution:
p(x) = x−5
⇒ x−5 = 0
⇒ x = 5
∴ 5 is a zero polynomial of the polynomial p(x).
(iii) p(x) = 2x+5
Solution:
p(x) = 2x+5
⇒ 2x+5 = 0
⇒ 2x = −5
⇒ x = -5/2
∴x = -5/2 is a zero polynomial of the polynomial p(x).
(iv) p(x) = 3x–2
Solution:
p(x) = 3x–2
⇒ 3x−2 = 0
⇒ 3x = 2
⇒x = 2/3
∴ x = 2/3 is a zero polynomial of the polynomial p(x).
(v) p(x) = 3x
Solution:
p(x) = 3x
⇒ 3x = 0
⇒ x = 0
∴ 0 is a zero polynomial of the polynomial p(x).
(vi) p(x) = ax, a≠0
Solution:
p(x) = ax
⇒ ax = 0
⇒ x = 0
∴ x = 0 is a zero polynomial of the polynomial p(x).
(vii) p(x) = cx+d, c ≠ 0, c, d are real numbers.
Solution:
p(x) = cx + d
⇒ cx+d =0
⇒ x = -d/c
∴ x = -d/c is a zero polynomial of the polynomial p(x).
Ncert Solution For Class 9 Maths Chapter – 2
Exercise 2.3
Question 1. Find the remainder when x3+3x2+3x+1 is divided by
(i) x+1
Solution:
x+1= 0
⇒x = −1
∴ Remainder:
p(−1) = (−1)3+3(−1)2+3(−1)+1
= −1+3−3+1
= 0
(ii) x−1/2
Solution:
x-1/2 = 0
⇒ x = 1/2
∴ Remainder:
p(1/2) = (1/2)3+3(1/2)2+3(1/2)+1
= (1/8)+(3/4)+(3/2)+1
= 27/8
(iii) x
Solution:
x = 0
p(x) = x3−ax2+6x−a
x−a = 0
∴ x = a
Remainder:
p(a) = (a)3−a(a2)+6(a)−a
= a3−a3+6a−a = 5a
Question 3. Check whether 7+3x is a factor of 3x3+7x.
Solution:
7+3x = 0
⇒ 3x = −7
⇒ x = -7/3
∴ Remainder:
3(-7/3)3+7(-7/3) = -(343/9)+(-49/3)
= (-343-(49)3)/9
= (-343-147)/9
= -490/9 ≠ 0
∴ 7+3x is not a factor of 3x3+7x
Ncert Solution For Class 9 Maths Chapter – 2
Exercise 2.4
1. Determine which of the following polynomials has (x + 1) a factor:
(i) x3+x2+x+1
Solution:
Let p(x) = x3+x2+x+1
The zero of x+1 is -1. [x+1 = 0 means x = -1]
p(−1) = (−1)3+(−1)2+(−1)+1
= −1+1−1+1
= 0
∴By factor theorem, x+1 is a factor of x3+x2+x+1
(ii) x4+x3+x2+x+1
Solution:
Let p(x)= x4+x3+x2+x+1
The zero of x+1 is -1. . [x+1= 0 means x = -1]
p(−1) = (−1)4+(−1)3+(−1)2+(−1)+1
= 1−1+1−1+1
= 1 ≠ 0
∴By factor theorem, x+1 is not a factor of x4 + x3 + x2 + x + 1
(iii) x4+3x3+3x2+x+1
Solution:
Let p(x)= x4+3x3+3x2+x+1
The zero of x+1 is -1.
p(−1)=(−1)4+3(−1)3+3(−1)2+(−1)+1
=1−3+3−1+1
=1 ≠ 0
∴By factor theorem, x+1 is not a factor of x4+3x3+3x2+x+1
(iv) x3 – x2– (2+√2)x +√2
Solution:
Let p(x) = x3–x2–(2+√2)x +√2
The zero of x+1 is -1.
p(−1) = (-1)3–(-1)2–(2+√2)(-1) + √2 = −1−1+2+√2+√2
= 2√2 ≠ 0
∴By factor theorem, x+1 is not a factor of x3–x2–(2+√2)x +√2
2. Use the Factor Theorem to determine whether g(x) is a factor of p(x) in each of the following cases:
(i) p(x) = 2x3+x2–2x–1, g(x) = x+1
Solution:
p(x) = 2x3+x2–2x–1, g(x) = x+1
g(x) = 0
⇒ x+1 = 0
⇒ x = −1
∴Zero of g(x) is -1.
Now,
p(−1) = 2(−1)3+(−1)2–2(−1)–1
= −2+1+2−1
= 0
∴By factor theorem, g(x) is a factor of p(x).
(ii) p(x)=x3+3x2+3x+1, g(x) = x+2
Solution:
p(x) = x3+3x2+3x+1, g(x) = x+2
g(x) = 0
⇒ x+2 = 0
⇒ x = −2
∴ Zero of g(x) is -2.
Now,
p(−2) = (−2)3+3(−2)2+3(−2)+1
= −8+12−6+1
= −1 ≠ 0
∴By factor theorem, g(x) is not a factor of p(x).
(iii) p(x)=x3–4x2+x+6, g(x) = x–3
Solution:
p(x) = x3–4x2+x+6, g(x) = x -3
g(x) = 0
⇒ x−3 = 0
⇒ x = 3
∴ Zero of g(x) is 3.
Now,
p(3) = (3)3−4(3)2+(3)+6
= 27−36+3+6
= 0
∴By factor theorem, g(x) is a factor of p(x).
3. Find the value of k, if x–1 is a factor of p(x) in each of the following cases:
(i) p(x) = x2+x+k
Solution:
If x-1 is a factor of p(x), then p(1) = 0
By Factor Theorem
⇒ (1)2+(1)+k = 0
⇒ 1+1+k = 0
⇒ 2+k = 0
⇒ k = −2
(ii) p(x) = 2x2+kx+√2
Solution:
If x-1 is a factor of p(x), then p(1)=0
⇒ 2(1)2+k(1)+√2 = 0
⇒ 2+k+√2 = 0
⇒ k = −(2+√2)
(iii) p(x) = kx2–√2x+1
Solution:
If x-1 is a factor of p(x), then p(1)=0
By Factor Theorem
⇒ k(1)2-√2(1)+1=0
⇒ k = √2-1
(iv) p(x)=kx2–3x+k
Solution:
If x-1 is a factor of p(x), then p(1) = 0
By Factor Theorem
⇒ k(1)2–3(1)+k = 0
⇒ k−3+k = 0
⇒ 2k−3 = 0
⇒ k= 3/2
4. Factorize:
(i) 12x2–7x+1
Solution:
Using the splitting the middle term method,
We have to find a number whose sum = -7 and product =1×12 = 12
We get -3 and -4 as the numbers [-3+-4=-7 and -3×-4 = 12]
12x2–7x+1= 12x2-4x-3x+1
= 4x(3x-1)-1(3x-1)
= (4x-1)(3x-1)
(ii) 2x2+7x+3
Solution:
Using the splitting the middle term method,
We have to find a number whose sum = 7 and product = 2×3 = 6
We get 6 and 1 as the numbers [6+1 = 7 and 6×1 = 6]
2x2+7x+3 = 2x2+6x+1x+3
= 2x (x+3)+1(x+3)
= (2x+1)(x+3)
(iii) 6x2+5x-6
Solution:
Using the splitting the middle term method,
We have to find a number whose sum = 5 and product = 6×-6 = -36
We get -4 and 9 as the numbers [-4+9 = 5 and -4×9 = -36]
6x2+5x-6 = 6x2+9x–4x–6
= 3x(2x+3)–2(2x+3)
= (2x+3)(3x–2)
(iv) 3x2–x–4
Solution:
Using the splitting the middle term method,
We have to find a number whose sum = -1 and product = 3×-4 = -12
We get -4 and 3 as the numbers [-4+3 = -1 and -4×3 = -12]
3x2–x–4 = 3x2–4x+3x–4
= x(3x–4)+1(3x–4)
= (3x–4)(x+1)
5. Factorize:
(i) x3–2x2–x+2
Solution:
Let p(x) = x3–2x2–x+2
Factors of 2 are ±1 and ± 2
Now,
p(x) = x3–2x2–x+2
p(−1) = (−1)3–2(−1)2–(−1)+2
= −1−2+1+2
= 0
Therefore, (x+1) is the factor of p(x)
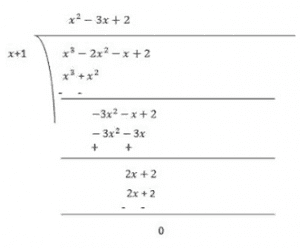
Now, Dividend = Divisor × Quotient + Remainder
(x+1)(x2–3x+2) = (x+1)(x2–x–2x+2)
= (x+1)(x(x−1)−2(x−1))
= (x+1)(x−1)(x-2)
(ii) x3–3x2–9x–5
Solution:
Let p(x) = x3–3x2–9x–5
Factors of 5 are ±1 and ±5
By trial method, we find that
p(5) = 0
So, (x-5) is factor of p(x)
Now,
p(x) = x3–3x2–9x–5
p(5) = (5)3–3(5)2–9(5)–5
= 125−75−45−5
= 0
Therefore, (x-5) is the factor of p(x)
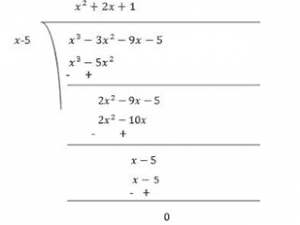
Now, Dividend = Divisor × Quotient + Remainder
(x−5)(x2+2x+1) = (x−5)(x2+x+x+1)
= (x−5)(x(x+1)+1(x+1))
= (x−5)(x+1)(x+1)
(iii) x3+13x2+32x+20
Solution:
Let p(x) = x3+13x2+32x+20
Factors of 20 are ±1, ±2, ±4, ±5, ±10 and ±20
By trial method, we find that
p(-1) = 0
So, (x+1) is factor of p(x)
Now,
p(x)= x3+13x2+32x+20
p(-1) = (−1)3+13(−1)2+32(−1)+20
= −1+13−32+20
= 0
Therefore, (x+1) is the factor of p(x)
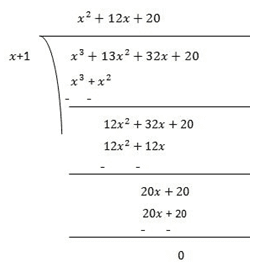
Now, Dividend = Divisor × Quotient +Remainder
(x+1)(x2+12x+20) = (x+1)(x2+2x+10x+20)
= (x+1)x(x+2)+10(x+2)
= (x+1)(x+2)(x+10)
(iv) 2y3+y2–2y–1
Solution:
Let p(y) = 2y3+y2–2y–1
Factors = 2×(−1)= -2 are ±1 and ±2
By trial method, we find that
p(1) = 0
So, (y-1) is factor of p(y)
Now,
p(y) = 2y3+y2–2y–1
p(1) = 2(1)3+(1)2–2(1)–1
= 2+1−2
= 0
Therefore, (y-1) is the factor of p(y)

Now, Dividend = Divisor × Quotient + Remainder
(y−1)(2y2+3y+1) = (y−1)(2y2+2y+y+1)
= (y−1)(2y(y+1)+1(y+1))
= (y−1)(2y+1)(y+1)
Ncert Solution For Class 9 Maths Chapter – 2
Exercise 2.5
Question 1. Use suitable identities to find the following products:
(i) (x+4)(x +10)
Solution:
Using the identity, (x+a)(x+b) = x 2+(a+b)x+ab
[Here, a = 4 and b = 10]
We get,
(x+4)(x+10) = x2+(4+10)x+(4×10)
= x2+14x+40
(ii) (x+8)(x –10)
Solution:
Using the identity, (x+a)(x+b) = x 2+(a+b)x+ab
[Here, a = 8 and b = −10]
We get,
(x+8)(x−10) = x2+(8+(−10))x+(8×(−10))
= x2+(8−10)x–80
= x2−2x−80
(iii) (3x+4)(3x–5)
Solution:
Using the identity, (x+a)(x+b) = x 2+(a+b)x+ab
[Here, x = 3x, a = 4 and b = −5]
We get,
(3x+4)(3x−5) = (3x)2+[4+(−5)]3x+4×(−5)
= 9x2+3x(4–5)–20
= 9x2–3x–20
(iv) (y2+3/2)(y2-3/2)
Solution:
Using the identity, (x+y)(x–y) = x2–y 2
[Here, x = y2and y = 3/2]
We get,
(y2+3/2)(y2–3/2) = (y2)2–(3/2)2
= y4–9/4
Question 2. Evaluate the following products without multiplying directly:
(i) 103×107
Solution:
103×107= (100+3)×(100+7)
Using identity, [(x+a)(x+b) = x2+(a+b)x+ab
Here, x = 100
a = 3
b = 7
We get, 103×107 = (100+3)×(100+7)
= (100)2+(3+7)100+(3×7)
= 10000+1000+21
= 11021
(ii) 95×96
Solution:
95×96 = (100-5)×(100-4)
Using identity, [(x-a)(x-b) = x2-(a+b)x+ab
Here, x = 100
a = -5
b = -4
We get, 95×96 = (100-5)×(100-4)
= (100)2+100(-5+(-4))+(-5×-4)
= 10000-900+20
= 9120
(iii) 104×96
Solution:
104×96 = (100+4)×(100–4)
Using identity, [(a+b)(a-b)= a2-b2]
Here, a = 100
b = 4
We get, 104×96 = (100+4)×(100–4)
= (100)2–(4)2
= 10000–16
= 9984
Question 3. Factorise the following using appropriate identities:
(i) 9x2+6xy+y2
Solution:
9x2+6xy+y2 = (3x)2+(2×3x×y)+y2
Using identity, x2+2xy+y2 = (x+y)2
Here, x = 3x
y = y
9x2+6xy+y2 = (3x)2+(2×3x×y)+y2
= (3x+y)2
= (3x+y)(3x+y)
(ii) 4y2−4y+1
Solution:
4y2−4y+1 = (2y)2–(2×2y×1)+1
Using identity, x2 – 2xy + y2 = (x – y)2
Here, x = 2y
y = 1
4y2−4y+1 = (2y)2–(2×2y×1)+12
= (2y–1)2
= (2y–1)(2y–1)
(iii) x2–y2/100
Solution:
x2–y2/100 = x2–(y/10)2
Using identity, x2-y2 = (x-y)(x+y)
Here, x = x
y = y/10
x2–y2/100 = x2–(y/10)2
= (x–y/10)(x+y/10)
Question 4. Expand each of the following using suitable identities:
(i) (x+2y+4z)2
(ii) (2x−y+z)2
(iii) (−2x+3y+2z)2
(iv) (3a –7b–c)2
(v) (–2x+5y–3z)2
(vi) ((1/4)a-(1/2)b +1)2
Solution:
(i) (x+2y+4z)2
Using identity, (x+y+z)2 = x2+y2+z2+2xy+2yz+2zx
Here, x = x
y = 2y
z = 4z
(x+2y+4z)2 = x2+(2y)2+(4z)2+(2×x×2y)+(2×2y×4z)+(2×4z×x)
= x2+4y2+16z2+4xy+16yz+8xz
(ii) (2x−y+z)2
Using identity, (x+y+z)2 = x2+y2+z2+2xy+2yz+2zx
Here, x = 2x
y = −y
z = z
(2x−y+z)2 = (2x)2+(−y)2+z2+(2×2x×−y)+(2×−y×z)+(2×z×2x)
= 4x2+y2+z2–4xy–2yz+4xz
(iii) (−2x+3y+2z)2
Solution:
Using identity, (x+y+z)2 = x2+y2+z2+2xy+2yz+2zx
Here, x = −2x
y = 3y
z = 2z
(−2x+3y+2z)2 = (−2x)2+(3y)2+(2z)2+(2×−2x×3y)+(2×3y×2z)+(2×2z×−2x)
= 4x2+9y2+4z2–12xy+12yz–8xz
(iv) (3a –7b–c)2
Solution:
Using identity (x+y+z)2 = x2+y2+z2+2xy+2yz+2zx
Here, x = 3a
y = – 7b
z = – c
(3a –7b– c)2 = (3a)2+(– 7b)2+(– c)2+(2×3a ×– 7b)+(2×– 7b ×– c)+(2×– c ×3a)
= 9a2 + 49b2 + c2– 42ab+14bc–6ca
(v) (–2x+5y–3z)2
Solution:
Using identity, (x+y+z)2 = x2+y2+z2+2xy+2yz+2zx
Here, x = –2x
y = 5y
z = – 3z
(–2x+5y–3z)2 = (–2x)2+(5y)2+(–3z)2+(2×–2x × 5y)+(2× 5y×– 3z)+(2×–3z ×–2x)
= 4x2+25y2 +9z2– 20xy–30yz+12zx
(vi) ((1/4)a-(1/2)b+1)2
Solution:
Using identity, (x+y+z)2 = x2+y2+z2+2xy+2yz+2zx
Here, x = (1/4)a
y = (-1/2)b
z = 1
Questin 5. Factorise:
(i) 4x2+9y2+16z2+12xy–24yz–16xz
(ii) 2x2+y2+8z2–2√2xy+4√2yz–8xz
Solution:
(i) 4x2+9y2+16z2+12xy–24yz–16xz
Using identity, (x+y+z)2 = x2+y2+z2+2xy+2yz+2zx
We can say that, x2+y2+z2+2xy+2yz+2zx = (x+y+z)2
4x2+9y2+16z2+12xy–24yz–16xz = (2x)2+(3y)2+(−4z)2+(2×2x×3y)+(2×3y×−4z)+(2×−4z×2x)
= (2x+3y–4z)2
= (2x+3y–4z)(2x+3y–4z)
(ii) 2x2+y2+8z2–2√2xy+4√2yz–8xz
Using identity, (x +y+z)2 = x2+y2+z2+2xy+2yz+2zx
We can say that, x2+y2+z2+2xy+2yz+2zx = (x+y+z)2
2x2+y2+8z2–2√2xy+4√2yz–8xz
= (-√2x)2+(y)2+(2√2z)2+(2×-√2x×y)+(2×y×2√2z)+(2×2√2×−√2x)
= (−√2x+y+2√2z)2
= (−√2x+y+2√2z)(−√2x+y+2√2z)
Question 6. Write the following cubes in expanded form:
(i) (2x+1)3
(ii) (2a−3b)3
(iii) ((3/2)x+1)3
(iv) (x−(2/3)y)3
Solution:
(i) (2x+1)3
Using identity,(x+y)3 = x3+y3+3xy(x+y)
(2x+1)3= (2x)3+13+(3×2x×1)(2x+1)
= 8x3+1+6x(2x+1)
= 8x3+12x2+6x+1
(ii) (2a−3b)3
Using identity,(x–y)3 = x3–y3–3xy(x–y)
(2a−3b)3 = (2a)3−(3b)3–(3×2a×3b)(2a–3b)
= 8a3–27b3–18ab(2a–3b)
= 8a3–27b3–36a2b+54ab2
(iii) ((3/2)x+1)3
Using identity,(x+y)3 = x3+y3+3xy(x+y)
((3/2)x+1)3=((3/2)x)3+13+(3×(3/2)x×1)((3/2)x +1)
(iv) (x−(2/3)y)3
Using identity, (x –y)3 = x3–y3–3xy(x–y)
- Evaluate the following using suitable identities:
(i) (99)3
(ii) (102)3
(iii) (998)3
Solutions:
(i) (99)3
Solution:
We can write 99 as 100–1
Using identity, (x –y)3 = x3–y3–3xy(x–y)
(99)3 = (100–1)3
= (100)3–13–(3×100×1)(100–1)
= 1000000 –1–300(100 – 1)
= 1000000–1–30000+300
= 970299
(ii) (102)3
Solution:
We can write 102 as 100+2
Using identity,(x+y)3 = x3+y3+3xy(x+y)
(100+2)3 =(100)3+23+(3×100×2)(100+2)
= 1000000 + 8 + 600(100 + 2)
= 1000000 + 8 + 60000 + 1200
= 1061208
(iii) (998)3
Solution:
We can write 99 as 1000–2
Using identity,(x–y)3 = x3–y3–3xy(x–y)
(998)3 =(1000–2)3
=(1000)3–23–(3×1000×2)(1000–2)
= 1000000000–8–6000(1000– 2)
= 1000000000–8- 6000000+12000
= 994011992
Question 8. Factorise each of the following:
(i) 8a3+b3+12a2b+6ab2
(ii) 8a3–b3–12a2b+6ab2
(iii) 27–125a3–135a +225a2
(iv) 64a3–27b3–144a2b+108ab2
(v) 27p3–(1/216)−(9/2) p2+(1/4)p
Solutions:
(i) 8a3+b3+12a2b+6ab2
Solution:
The expression, 8a3+b3+12a2b+6ab2 can be written as (2a)3+b3+3(2a)2b+3(2a)(b)2
8a3+b3+12a2b+6ab2 = (2a)3+b3+3(2a)2b+3(2a)(b)2
= (2a+b)3
= (2a+b)(2a+b)(2a+b)
Here, the identity, (x +y)3 = x3+y3+3xy(x+y) is used.
(ii) 8a3–b3–12a2b+6ab2
Solution:
The expression, 8a3–b3−12a2b+6ab2 can be written as (2a)3–b3–3(2a)2b+3(2a)(b)2
8a3–b3−12a2b+6ab2 = (2a)3–b3–3(2a)2b+3(2a)(b)2
= (2a–b)3
= (2a–b)(2a–b)(2a–b)
Here, the identity,(x–y)3 = x3–y3–3xy(x–y) is used.
(iii) 27–125a3–135a+225a2
Solution:
The expression, 27–125a3–135a +225a2 can be written as 33–(5a)3–3(3)2(5a)+3(3)(5a)2
27–125a3–135a+225a2 =
33–(5a)3–3(3)2(5a)+3(3)(5a)2
= (3–5a)3
= (3–5a)(3–5a)(3–5a)
Here, the identity, (x–y)3 = x3–y3-3xy(x–y) is used.
(iv) 64a3–27b3–144a2b+108ab2
Solution:
The expression, 64a3–27b3–144a2b+108ab2can be written as (4a)3–(3b)3–3(4a)2(3b)+3(4a)(3b)2
64a3–27b3–144a2b+108ab2=
(4a)3–(3b)3–3(4a)2(3b)+3(4a)(3b)2
=(4a–3b)3
=(4a–3b)(4a–3b)(4a–3b)
Here, the identity, (x – y)3 = x3 – y3 – 3xy(x – y) is used.
(v) 27p3– (1/216)−(9/2) p2+(1/4)p
Solution:
The expression, 27p3–(1/216)−(9/2) p2+(1/4)p can be written as
(3p)3–(1/6)3−(9/2) p2+(1/4)p = (3p)3–(1/6)3−3(3p)(1/6)(3p – 1/6)
Using (x – y)3 = x3 – y3 – 3xy (x – y)
27p3–(1/216)−(9/2) p2+(1/4)p = (3p)3–(1/6)3−3(3p)(1/6)(3p – 1/6)
Taking x = 3p and y = 1/6
= (3p–1/6)3
= (3p–1/6)(3p–1/6)(3p–1/6)
Question 9. Verify:
(i) x3+y3 = (x+y)(x2–xy+y2)
(ii) x3–y3 = (x–y)(x2+xy+y2)
Solutions:
(i) x3+y3 = (x+y)(x2–xy+y2)
We know that, (x+y)3 = x3+y3+3xy(x+y)
⇒ x3+y3 = (x+y)3–3xy(x+y)
⇒ x3+y3 = (x+y)[(x+y)2–3xy]
Taking (x+y) common ⇒ x3+y3 = (x+y)[(x2+y2+2xy)–3xy]
⇒ x3+y3 = (x+y)(x2+y2–xy)
(ii) x3–y3 = (x–y)(x2+xy+y2)
We know that, (x–y)3 = x3–y3–3xy(x–y)
⇒ x3−y3 = (x–y)3+3xy(x–y)
⇒ x3−y3 = (x–y)[(x–y)2+3xy]
Taking (x+y) common ⇒ x3−y3 = (x–y)[(x2+y2–2xy)+3xy]
⇒ x3+y3 = (x–y)(x2+y2+xy)
Question 10. Factorise each of the following:
(i) 27y3+125z3
(ii) 64m3–343n3
Solutions:
(i) 27y3+125z3
The expression, 27y3+125z3 can be written as (3y)3+(5z)3
27y3+125z3 = (3y)3+(5z)3
We know that, x3+y3 = (x+y)(x2–xy+y2)
27y3+125z3 = (3y)3+(5z)3
= (3y+5z)[(3y)2–(3y)(5z)+(5z)2]
= (3y+5z)(9y2–15yz+25z2)
(ii) 64m3–343n3
The expression, 64m3–343n3can be written as (4m)3–(7n)3
64m3–343n3 =
(4m)3–(7n)3
We know that, x3–y3 = (x–y)(x2+xy+y2)
64m3–343n3 = (4m)3–(7n)3
= (4m-7n)[(4m)2+(4m)(7n)+(7n)2]
= (4m-7n)(16m2+28mn+49n2)
Question 11. Factorise: 27x3+y3+z3–9xyz.
Solution:
The expression 27x3+y3+z3–9xyz can be written as (3x)3+y3+z3–3(3x)(y)(z)
27x3+y3+z3–9xyz = (3x)3+y3+z3–3(3x)(y)(z)
We know that, x3+y3+z3–3xyz = (x+y+z)(x2+y2+z2–xy –yz–zx)
27x3+y3+z3–9xyz = (3x)3+y3+z3–3(3x)(y)(z)
= (3x+y+z)[(3x)2+y2+z2–3xy–yz–3xz]
= (3x+y+z)(9x2+y2+z2–3xy–yz–3xz)
Question 12. Verify that:
x3+y3+z3–3xyz = (1/2) (x+y+z)[(x–y)2+(y–z)2+(z–x)2]
Solution:
We know that,
x3+y3+z3−3xyz = (x+y+z)(x2+y2+z2–xy–yz–xz)
⇒ x3+y3+z3–3xyz = (1/2)(x+y+z)[2(x2+y2+z2–xy–yz–xz)]
= (1/2)(x+y+z)(2x2+2y2+2z2–2xy–2yz–2xz)
= (1/2)(x+y+z)[(x2+y2−2xy)+(y2+z2–2yz)+(x2+z2–2xz)]
= (1/2)(x+y+z)[(x–y)2+(y–z)2+(z–x)2]
Question 13. If x+y+z = 0, show that x3+y3+z3 = 3xyz.
Solution:
We know that,
x3+y3+z3-3xyz = (x +y+z)(x2+y2+z2–xy–yz–xz)
Now, according to the question, let (x+y+z) = 0,
Then, x3+y3+z3 -3xyz = (0)(x2+y2+z2–xy–yz–xz)
⇒ x3+y3+z3–3xyz = 0
⇒ x3+y3+z3 = 3xyz
Hence Prove
Question 14. Without actually calculating the cubes, find the value of each of the following:
(i) (−12)3+(7)3+(5)3
(ii) (28)3+(−15)3+(−13)3
Solution:
(i) (−12)3+(7)3+(5)3
Let a = −12
b = 7
c = 5
We know that if x+y+z = 0, then x3+y3+z3=3xyz.
Here, −12+7+5=0
(−12)3+(7)3+(5)3 = 3xyz
= 3×-12×7×5
= -1260
(ii) (28)3+(−15)3+(−13)3
Solution:
(28)3+(−15)3+(−13)3
Let a = 28
b = −15
c = −13
We know that if x+y+z = 0, then x3+y3+z3 = 3xyz.
Here, x+y+z = 28–15–13 = 0
(28)3+(−15)3+(−13)3 = 3xyz
= 0+3(28)(−15)(−13)
= 16380
Question 15. Give possible expressions for the length and breadth of each of the following rectangles, in which their areas are given:
(i) Area: 25a2–35a+12
(ii) Area: 35y2+13y–12
Solution:
(i) Area: 25a2–35a+12
Using the splitting the middle term method,
We have to find a number whose sum = -35 and product =25×12 = 300
We get -15 and -20 as the numbers [-15+-20=-35 and -15×-20 = 300]
25a2–35a+12 = 25a2–15a−20a+12
= 5a(5a–3)–4(5a–3)
= (5a–4)(5a–3)
Possible expression for length = 5a–4
Possible expression for breadth = 5a –3
(ii) Area: 35y2+13y–12
Using the splitting the middle term method,
We have to find a number whose sum = 13 and product = 35×-12 = 420
We get -15 and 28 as the numbers [-15+28 = 13 and -15×28=420]
35y2+13y–12 = 35y2–15y+28y–12
= 5y(7y–3)+4(7y–3)
= (5y+4)(7y–3)
Possible expression for length = (5y+4)
Possible expression for breadth = (7y–3)
Question 16. What are the possible expressions for the dimensions of the cuboids whose volumes are given below?
(i) Volume: 3x2–12x
(ii) Volume: 12ky2+8ky–20k
Solution:
(i) Volume: 3x2–12x
3x2–12x can be written as 3x(x–4) by taking 3x out of both the terms.
Possible expression for length = 3
Possible expression for breadth = x
Possible expression for height = (x–4)
(ii) Volume:
12ky2+8ky–20k
12ky2+8ky–20k can be written as 4k(3y2+2y–5) by taking 4k out of both the terms.
12ky2+8ky–20k = 4k(3y2+2y–5)
[Here, 3y2+2y–5 can be written as 3y2+5y–3y–5 using splitting the middle term method.]
= 4k(3y2+5y–3y–5)
= 4k[y(3y+5)–1(3y+5)]
= 4k(3y+5)(y–1)
Possible expression for length = 4k
Possible expression for breadth = (3y +5)
Possible expression for height = (y -1)
Ncert Solution For Class 9 Maths Chapter – 2
For the Next Chapter Solution Click Below
Chapter 3 – Coordinate Geometry
Chapter 4 – Linear Equations in Two Variables
Chapter 9 – Areas of Parallelograms and Triangles
Chapter 13 – Surface Areas and Volumes

